今回は、分数の掛け算(かけざん)のやり方と問題のとき方について書きたいと思います。 分数のかけ算のやり方 帯分数は仮分数に直してからかける 分子は分子どうしをかけ、分母は分母どうしをかける 計算をしながら約分できるときには約分をする 分数の掛け算問題と解き方 (adsbygoogle分数の掛け算と割り算の解き方 分数の掛け算と割り算を解きましょう。 複数の分数を掛け算するとき、分子と分母で割り算ができないか考えてください。割り算が可能なら、数を減らして「分母×分母」、「分子×分子」を計算します。答えを下記に示します。 分数の計算ドリル このページの この式を前から順に計算すると、答えは6になり正解です。 4÷4を先にすると、12×8÷(4÷4)=12×8÷1=96÷1=96となり不正解。 8÷4を先にすると、12×(8÷4)÷4=12×2÷4=24÷4=6となり正解。 また、(12÷4)×(8÷4)=3×2=6となり正解。
四則演算の順序 大人の学び直し算数 計算のやり方解説 無料
分数 掛け算 割り算 混合 解き方
分数 掛け算 割り算 混合 解き方-約分とは?1分でわかる意味、やり方、問題、約数、素因数分解との関係 分数の掛け算と割り算の解き方 分数の掛け算と割り算を解きましょう。 複数の分数を掛け算するとき、分子と分母で割り算ができないか考えてください。こんにちは、ウチダショウマです。 今日は、小学校高学年で習う 分数の割り算を掛け算にするときには、わる数の逆数(分数の分子と分母を入れかえる)をかけます。 ⇒ 分数の割り算やり方と問題 計算のとちゅうで約分できるので、約分をしてから計算をします。 × ÷ = × × = 答え




分数を使いこなそう かけ算 わり算と分数 後編 桜花 現役バイト塾講師 Note
分数の掛け算と割り算は下記も参考になります。 文字式の分数を掛け算するには?3分でわかる計算、問題、割り算との関係 分数とは?1分でわかる意味、分母、分子、約分、掛け算と割り算の解き方 100円から読める!ネット不要!印刷しても読みやすいpdf記事はこちら⇒ いつでもどこでも2 分数の割り算解き方のコツ 21 割る数を逆数にしてかける;分数のかけ算 分数×分数(1) 問題一括 (3,354Kb) 解答一括 (3,775Kb) 分数×分数(2) 力をつけよう(1) 力をつけよう(2) 4 分数のわり算 分数÷分数(1) 問題一括 (3,3Kb) 解答一括 (4,621Kb) 分数÷分数(2) 乗除混合 文章問題 分数の倍とかけ算・わり算(1) 分数の倍とかけ算・わり算(2)
分数の掛け算は、分子同士、分母同士をそれぞれ掛けることで計算します。 分数の掛け算の計算方法 \ \frac{a}{b}\times\frac{c}{d}=\frac{a\times c}{b\times d} \ 分数の計算(かけ算、割り算、引き算の混合) 問題集で、解答は(エ)となっているのですが、自分で計算すると(オ)となってしまいます。 どこを勘違いして、間違っているのかわかりません。 お分かりの方、教えてください。 この質問への回答は3 分数の割り算の応用 31 分数どうしの割り算;
⇒ 指数の掛け算や割り算や分数の計算問題の解き方 対数計算と指数計算はセットでやっておきましょう。 それほど難しい問題は出ないので、基本をおさえておけば目標点は取れるようになります。 例えこの分野の目標点が満点でもです。 ただし、 ⇒ 指数関数と対数関数の要点 グラフの分数同士の掛け算は、分子同士、分母同士をそれぞれ掛ける ことで計算できます。 次の例題を一緒に解いてみましょう。 2 3 × 1 5 2 3 × 1 5 を計算せよ。 この問題は、分数×分数の計算問題ですね。 分子同士の掛け算は、 2× 1 = 2 2 × 1 = 2 であり、分母同士の掛け算は、 3× 5 = 15 3 × 5 = 15 となります。 これらの掛け算の結果をそれぞれ、答えの分数の分子と分母にし帯分数の割り算 帯分数の割り算の場合は、帯分数を仮分数に直してから計算します。 分数の割り算は割る数を逆数にしてかければ良いだけ。 分数計算の考え方がしっかりわかっていれば、どんな帯分数が出てきても計算できてしまいますよ。 帯分数を



連立 方程式 計算 分数




単項式の除法 解き方のコツは分数の形にして文字を消すこと 中学や高校の数学の計算問題
分数の掛け算 分数の割り算の理解 割り算を表す記号について 1)「÷」 2)「/」 3)「:」 分数の割り算の理解その2(繁分数の利用) 問題 あきら君が乗っている自動車は、分でkm進みます。この自動車が一まず、2つの分数の分母「3」と「12」をそろえるために、 「2/3」の分子と分母四則混合計算の考え方については「四則混合 と考えます.②の番号は掛け算(×)に対してつけられているので逆算は割り算になります. つまり②の計算は『 9÷3=3 』となります. この結果を用いて次に①の逆算を実行します.①の計算は, となります.①の番号は足し算(+)に対して 1/3÷3/5=5/9=(1×5)/(3×3)=1/3×5/3 2/5÷3/7=14/15=(2×7)/(5×3)=2/5×7/3 中学生であれば、「分母をそろえる」方法を文字を用いて一般的に説明できるようになります。 b/a÷d/c= (bc/ac)÷ (ad/ac)=bc÷ad=bc/ad=b/a×c/d 以上、3つの考え方を紹介しました。 理解された方であれば「私ならこうタエ子に説明してあげる



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料




ルートの割り算の問題 やり方は を合体して中で割るだけだ 中学や高校の数学の計算問題
割り算の場合 割る数を逆数にして、掛け算に変えても 出てくる答えは同じという性質があります。 なので 数が割り切れない!という場合には この方法を用いて、分数として答えを出してやりま掛け算、割り算は、ルート同士、係数同士をそのまま計算します。 ルートの掛け算をしていると、ルートの数が大きくなっていきます。ルートの中の数が大きくなってきたときは整理していく、というルールがあります。 ルートの数はどうやって整理するの? ルートの中にある数は、2乗すれ割り算は逆数の掛け算と同じ なので分数の割り算はもちろん、整数の割り算も逆数の掛け算に直して計算する。 とくに、3数以上の計算や掛け算割り算の混ざった計算で有利になる。 まず割り算を逆数の掛け算に (+12) ÷(−8) = 12 ×(− 8 1) = − 8 12 2 3 = −




6 2 1 2 問題について教育委員会に問い合わせてみた 半月記



小数と分数が混じった式の解き方 大人の学び直し算数 計算のやり方解説 無料
掛け算、割り算が混じった計算では 割り算を逆数の掛け算 になおして計算する。 乗法だけの式なら、交換法則や結合法則が使えるが、乗法と除法が混じっているとそれらが使えず 計算の順序を間違えてミスが多くなる。 計算せよ。 (−12)÷(−9)÷(−3) (−24)÷(+16)×(−3)÷(2) ① (−12)÷(−9)÷分数とは?1分でわかる意味、分母、分子、約分、掛け算と割り算の解き方 割り算の意味は、下記が参考になります。 以上を通して見ると以下のようになります。 少し数式をいじってみましょう。四則計算 ツイート 小学生用の様々な計算のプリントを作りました。 無料でダウンロード・印刷できます。 お子さまの計算の力に合わせて、ご利用ください。 小学生の算数 足し算 練習問題プリント 無料ダウンロード・印刷 小学生の算数 引き算 練習




印刷可能 分数 掛け算 割り算 混合 ニスヌーピー 壁紙




小学6年生の算数 分数のわり算 分数 整数と分数 分数 練習問題プリント ちびむすドリル 小学生
1次方程式の解き方(まとめ) 小数、分数、かっこがあるときは、最初に処理しておきます。 1 係数に小数や分数があるときは、両辺を何倍かして整数係数に直しておきます。 2 「かっこ」があるときは、はずします。 上の処理が済んだら、次の手順で x=··の形に変形します。 (I) 「移項よく見られている電卓ページ 因数分解の電卓 入力された式を因数分解できる電卓です。解き方がいくつもある因数分解ですが、この電卓を使えば簡単に因数分解がおこなえます。 連立方程式の電卓 四則混合算の解き方は以下の2つです。 (1) ( )内を先に計算する。 (2) 掛け算、割り算を先に計算する。 つまり ( )の中の掛け算、割り算からスタートします。 ① (×1296÷48)×9/16×24÷3 = ()×9/16×24÷3 =2×9/16×24÷3= (2×9/16)×24÷3 = (9/8)×24÷3=27/3=9 ② (1
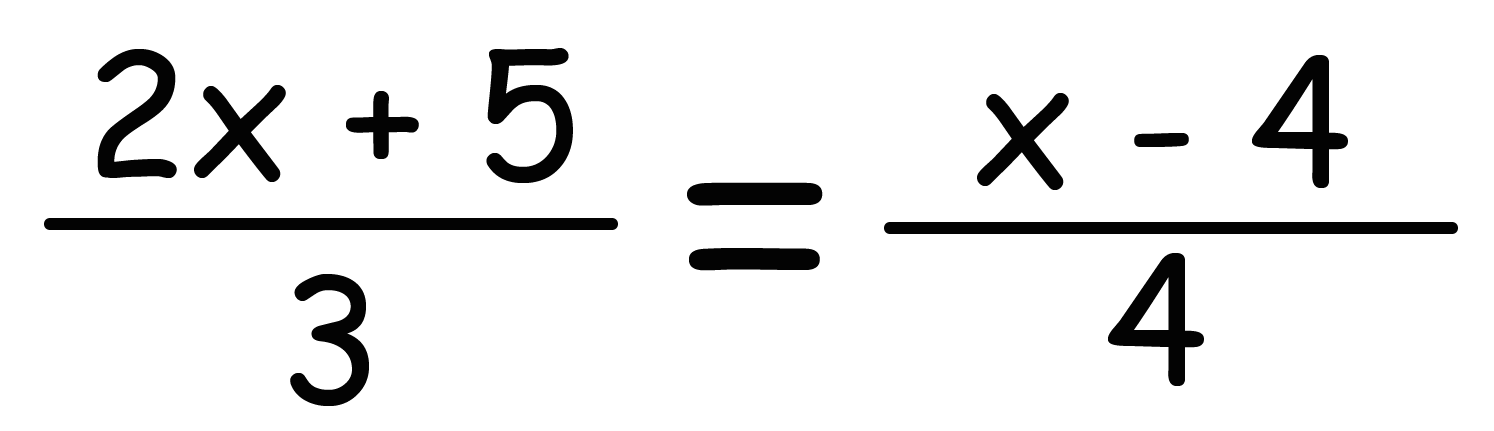



中1数学 分数をふくむ方程式の解き方 Qikeru 学びを楽しくわかりやすく
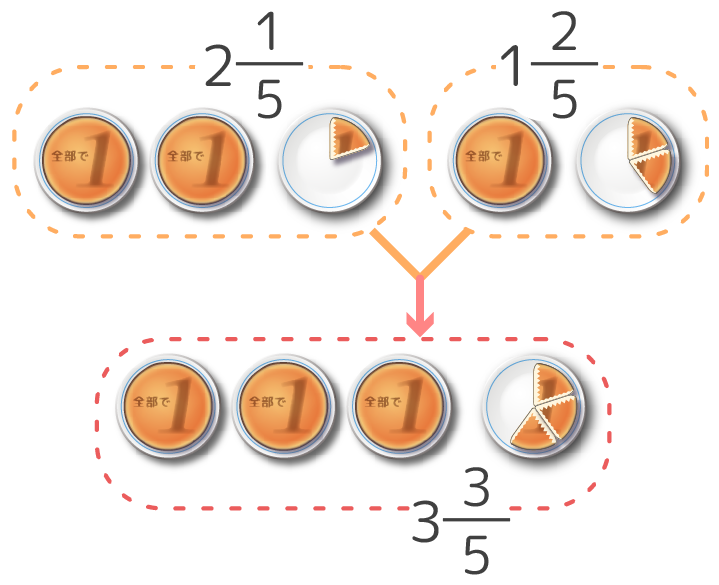



小学4年生 帯分数の足し算引き算 分数のくり上がり くり下がりも そうちゃ式 分かりやすい図解算数 別館
よく見られている電卓ページ 因数分解の電卓 入力された式を因数分解できる電卓です。解き方がいくつもある因数分解ですが、この電卓を使えば簡単に因数分解がおこなえます。 連立方程式の電卓 はてなブックマークやツイッター等で拡散していただけると、非常にウレシイです! ! こんにちは。 本日は 文字式の掛け算と割り算 の混合問題を紹介します。 a÷3×bを計算したとき、a、3、bのどれが分子と分母になるかをしっかり理解していきましょう! なお下のような字式の掛け算や割り算の解き方のポイントは、割り算がある場合は、すぐに逆数をとってまず 1 1 区画の面積に着目しましょう。 全体で 1m2 1 m 2 の土地を縦に 3 3 分割、横に 5 5 分割しているので、 15 15 分割しているのがわかります。 この区画が縦横にそれぞれ 2 2 つ分並べられたのが今回求める土地です。 1 15 m2 1 15 m 2 が 2× 2 2 × 2 で並んでいるので、 2 ×2 15 = 4 15(m2) 2 × 2 15 = 4 15 ( m 2) となります。 つまり、次のように分母同士・分子同士で掛け算し




算数 分数と小数の混じった計算方法とは 解き方を1から解説 数スタ




割り算を分数で表す問題 分数にするにはこれを覚えておけばok 中学や高校の数学の計算問題
こんな解き方もできる5の割り算の暗算のコツ 「分数と少数の対応表を利用した方法」シリーズで、今回は割る数が「5 17年10月30日 / 最終更新日 17年12月日 notty 割り算の暗算のコツ であれば、割り算を掛け算に直すことはできないのか?と考える これを『四則演算』といいます。 足し算は「+」、引き算は「-」、掛け算は「×」、割り算は「÷」の記号でそれぞれ表されることは、皆さんもよくご存じかと思います。 (例) 足し算:6+3=9 引き算:6-3=3 掛け算:6×3=18 割り算:6÷3=2 基本的に、数式は左から順に計算すればよく、いくつもの数字を繋げて長い式を作ることも可能です。 (例)
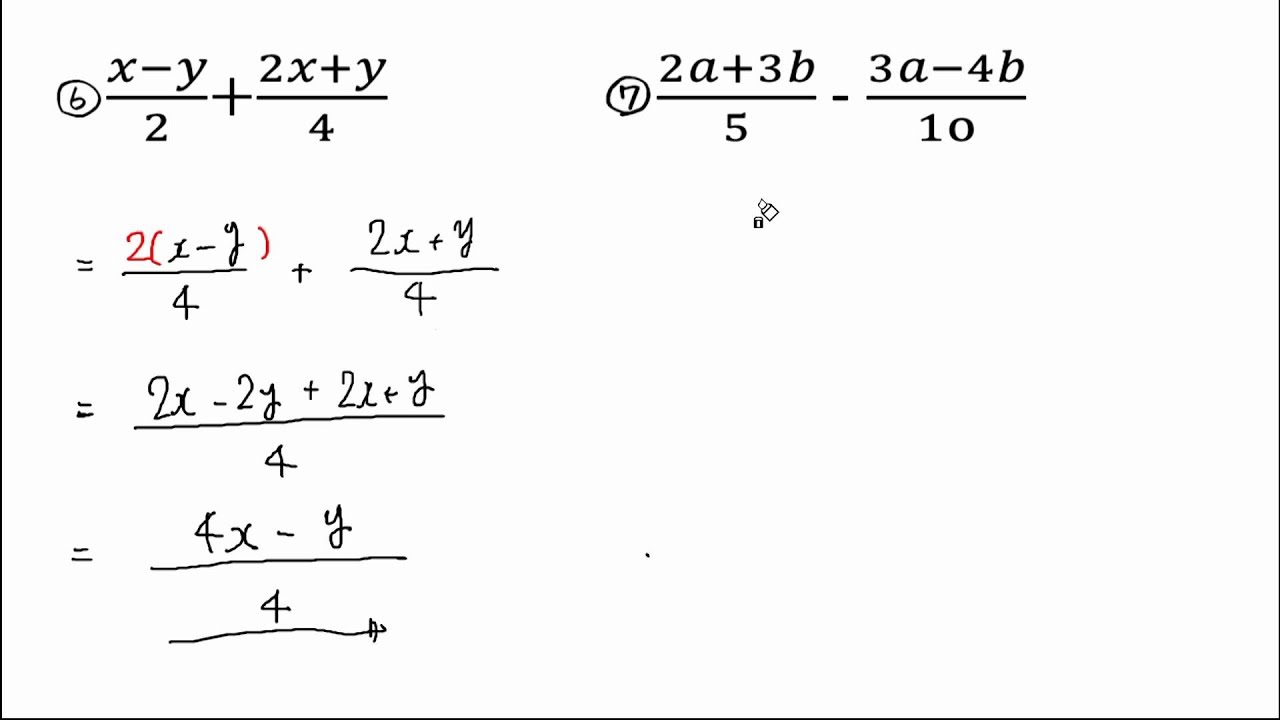



分数の入った文字式 Youtube



逆算の解き方 カテキョウブログ




分数の文字式と整数の掛け算 よく使う非常に大切な知識 中学や高校の数学の計算問題




割り算をしたとき その数は分母と分子のどっちに行くか覚えよう 中学や高校の数学の計算問題
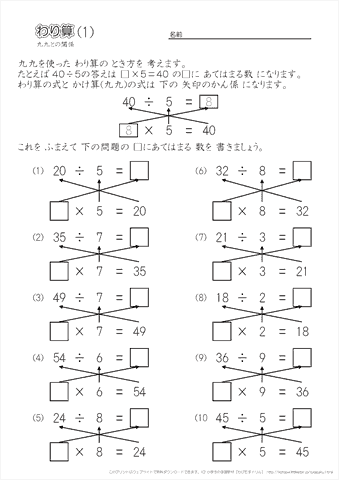



小学生の算数 わり算 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 小学生



四則演算の順序 大人の学び直し算数 計算のやり方解説 無料
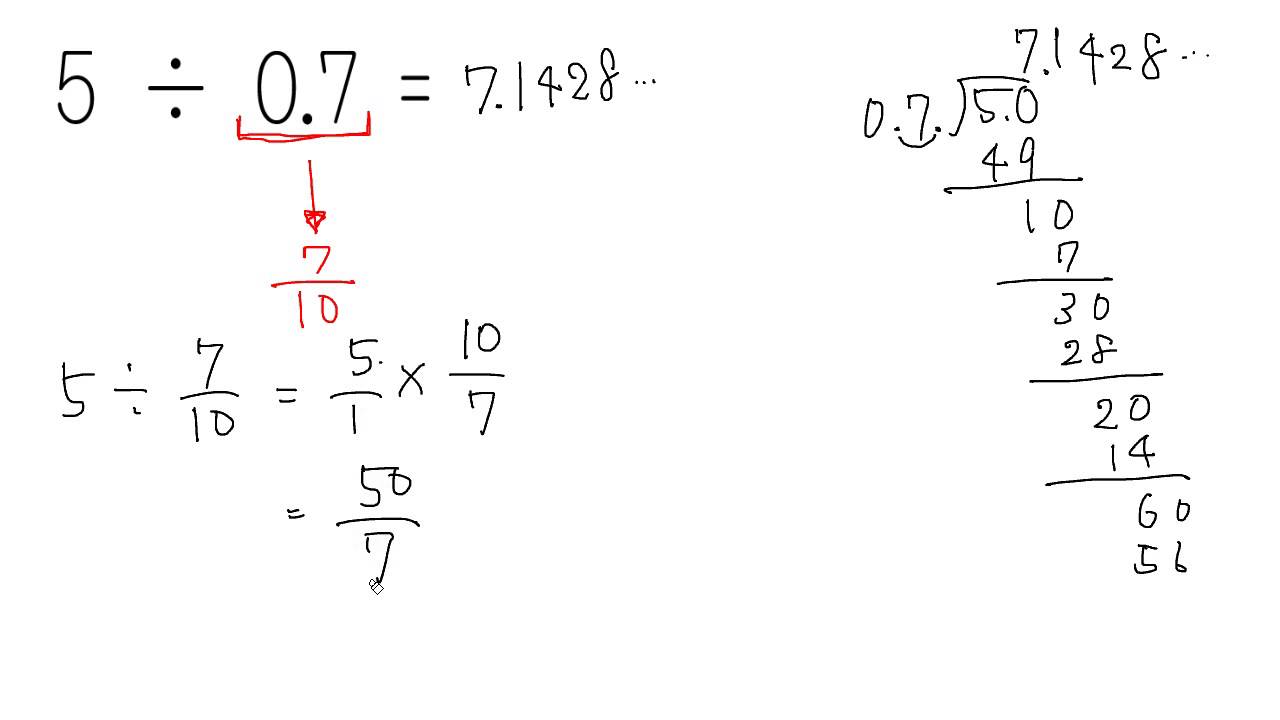



分数と小数の混じったかけ算 割り算 Youtube
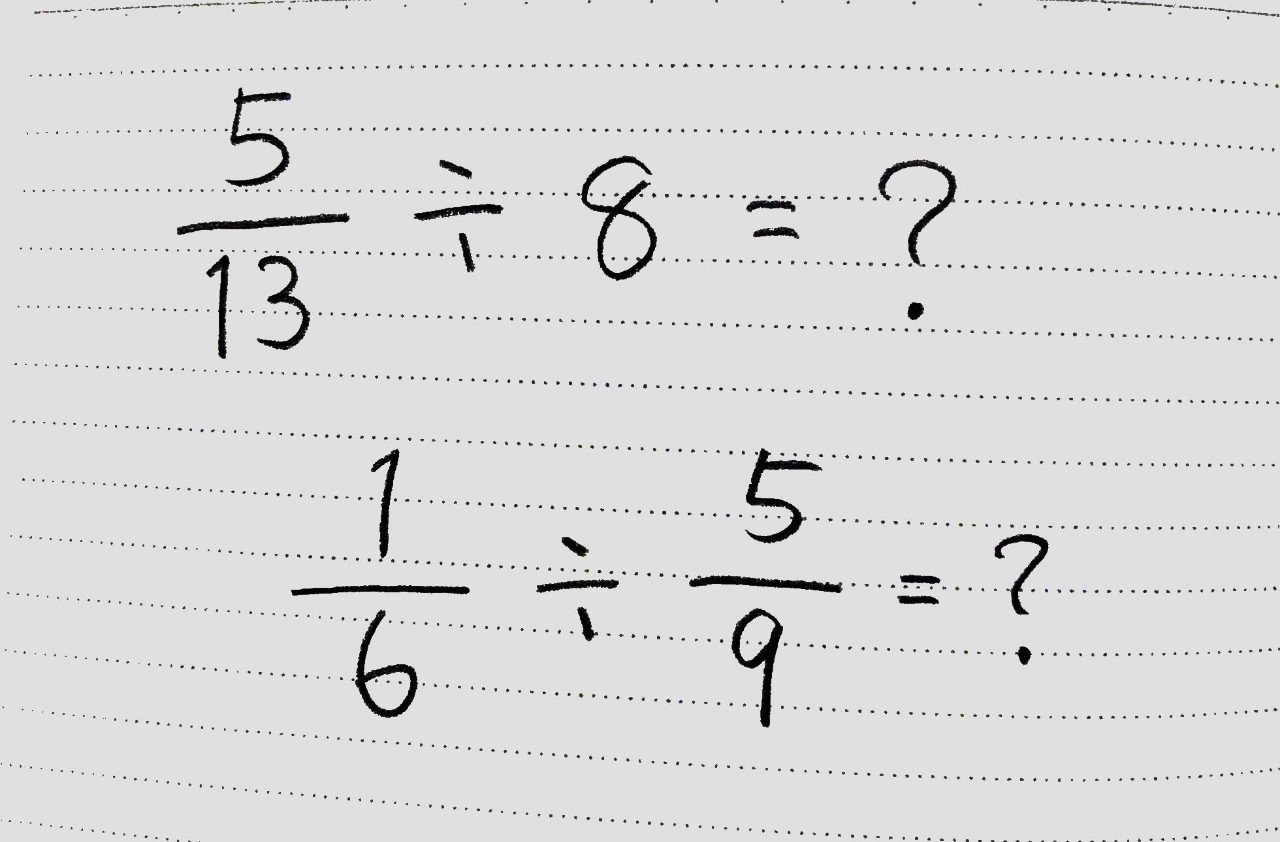



分数を使いこなそう かけ算 わり算と分数 後編 桜花 現役バイト塾講師 Note
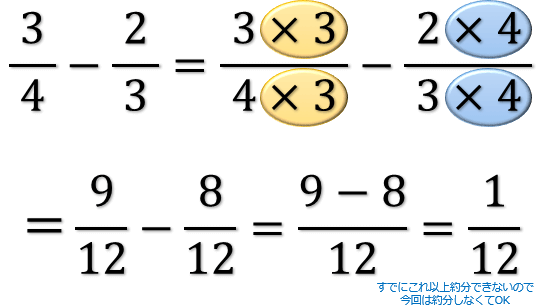



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ



1




小学6年生の算数 分数のわり算 分数 整数と分数 分数 練習問題プリント ちびむすドリル 小学生



小数と分数が混じった式の解き方 大人の学び直し算数 計算のやり方解説 無料
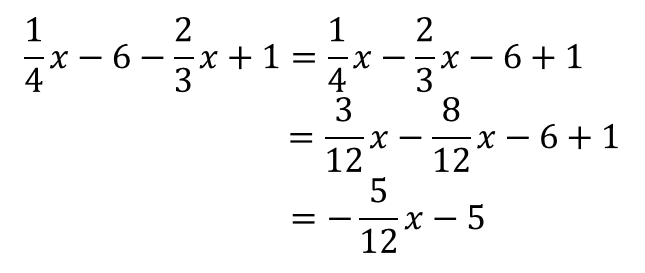



文字式 分数の計算問題を1から丁寧に 数スタ
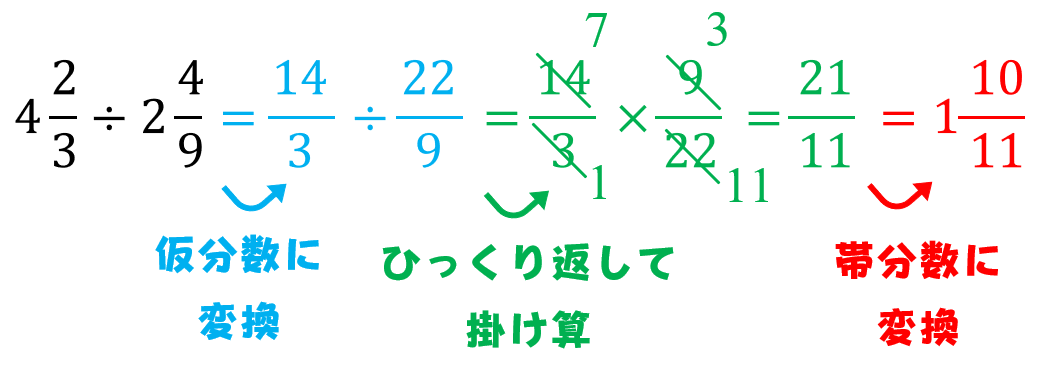



帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun




小6 分数と分数の割り算 のやり方は 逆数のかけ算になる理由 そうちゃ式 分かりやすい図解算数 別館




文字式の掛け算や割り算 割り算は掛け算に戻して計算しよう 中学や高校の数学の計算問題
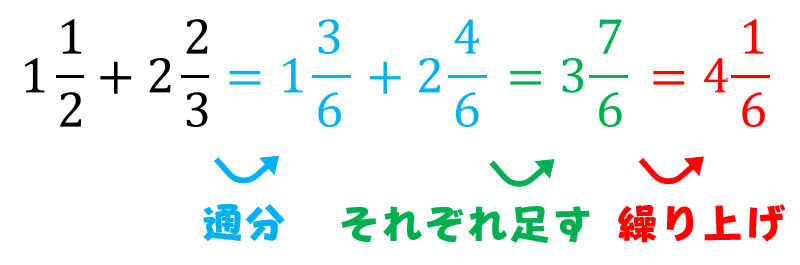



帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun




算数 分数と小数の混じった計算方法とは 解き方を1から解説 数スタ



平方根の割り算は 1分でわかる計算 割り算の問題とやり方 有理化 分数との関係



1



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料
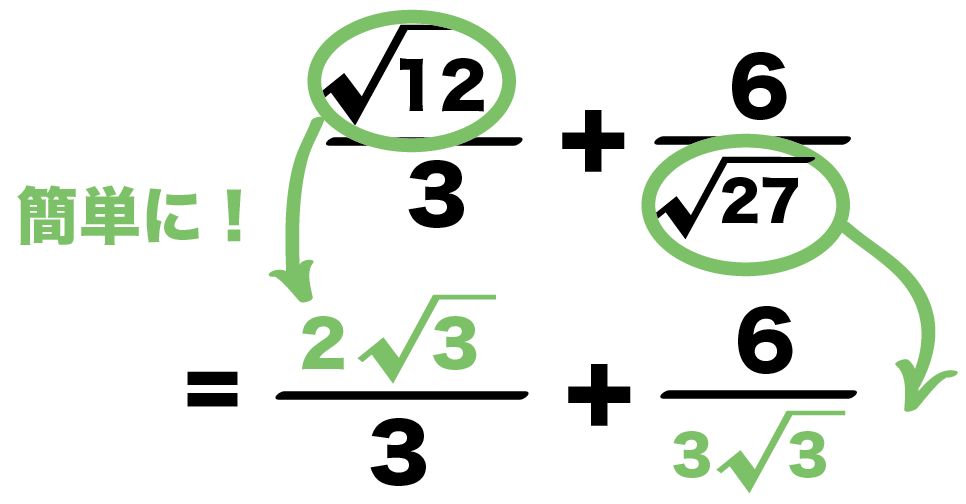



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
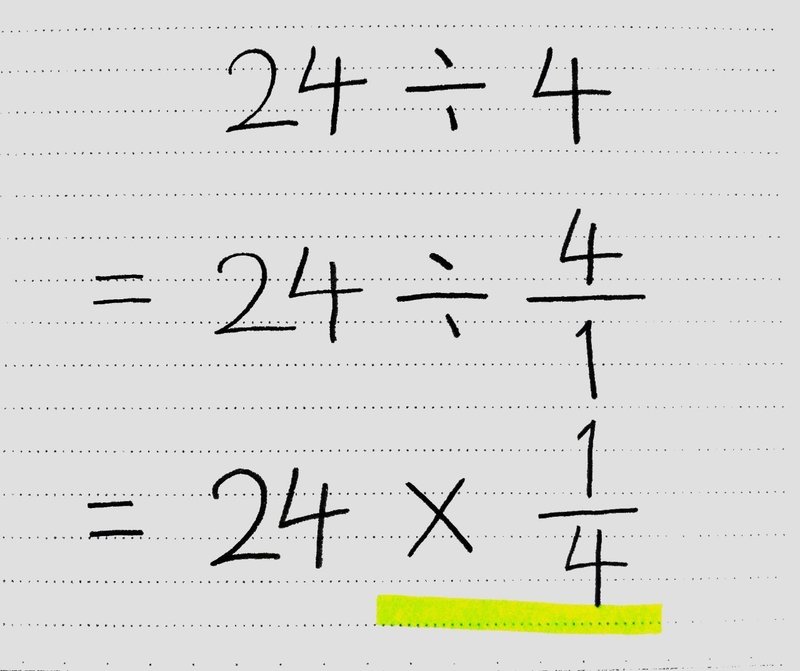



分数を使いこなそう かけ算 わり算と分数 後編 桜花 現役バイト塾講師 Note




中1 数学 中1 7 正負のかけ算 わり算 Youtube




分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ




分数の掛け算の上手な教え方 なぜ分母同士 分子同士をかけるのか 数学fun
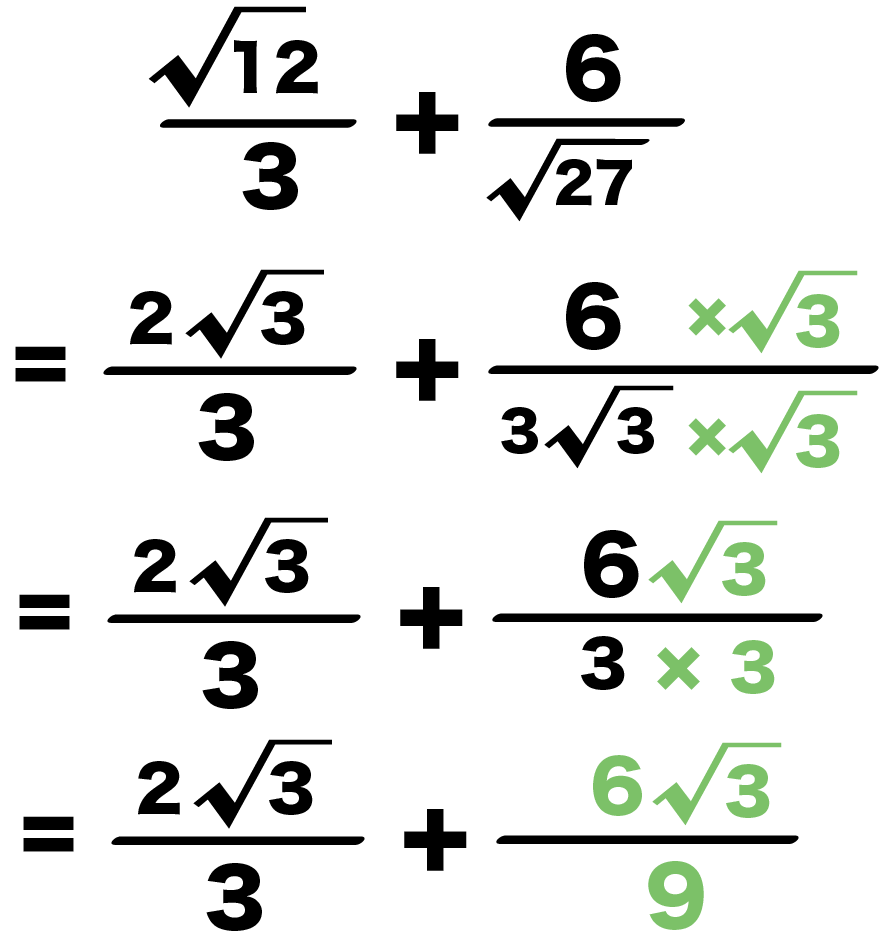



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
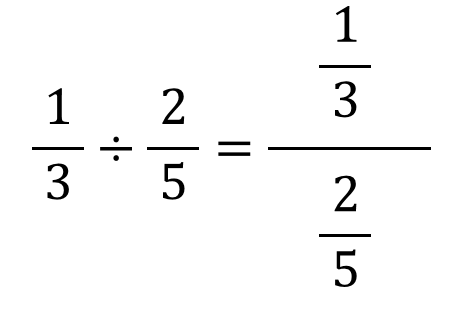



分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ




分数の割り算の問題 やり方は逆数をとってかけるだけ 中学や高校の数学の計算問題
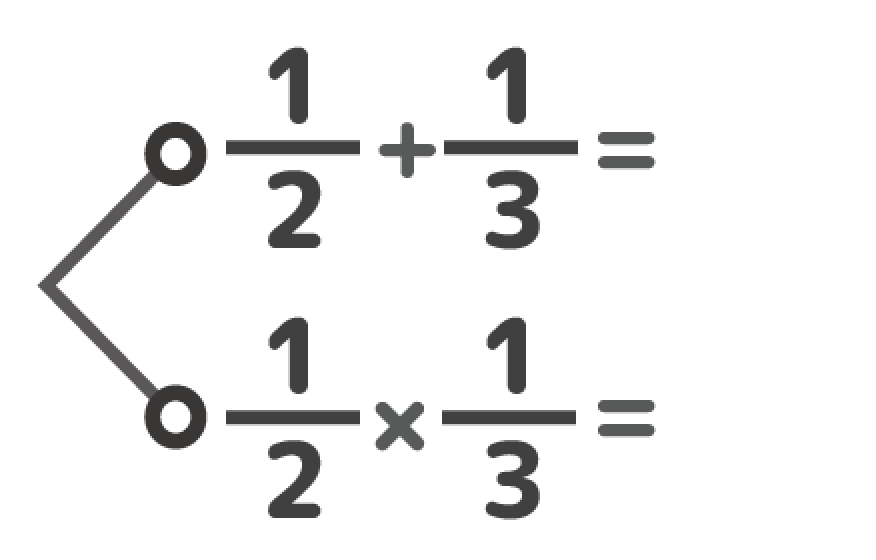



小6への分数の教え方のコツ 計算方法の違いを理解させる かけ算割り算と 算 算 そうちゃ式 分かりやすい図解算数 別館




平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ




分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ




分数を使いこなそう かけ算 わり算と分数 後編 桜花 現役バイト塾講師 Note
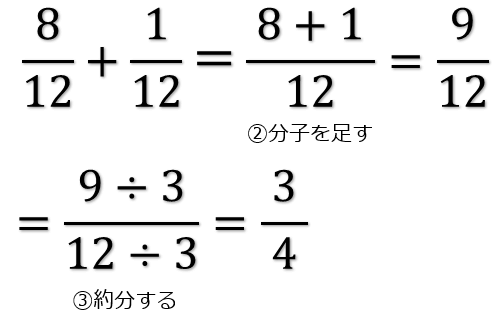



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ




分数のかけ算の計算プリント 帯分数編 全240問無料 算数パラダイス
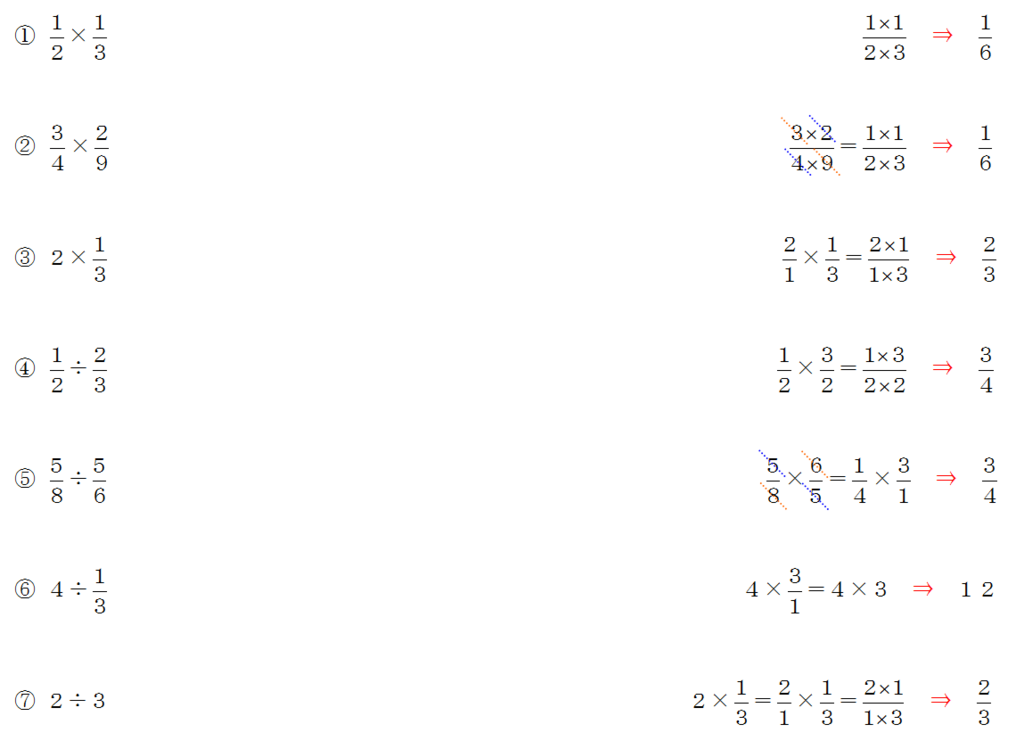



分数の掛け算や割り算の問題 計算のやり方は簡単だ 中学や高校の数学の計算問題




小6 算数 小6 5 分数のかけ算 Youtube
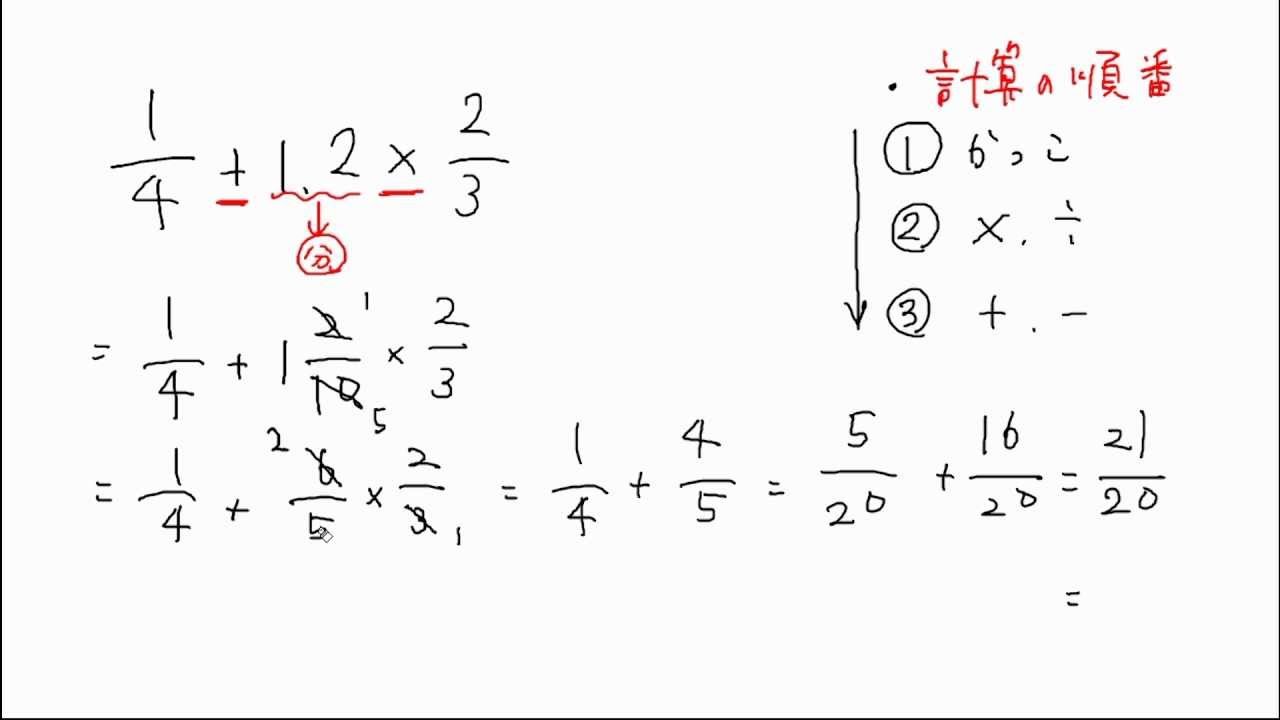



計算まとめ 四則の混じった計算1 Youtube




分数の割り算 やり方と問題 小学生 中学生の勉強
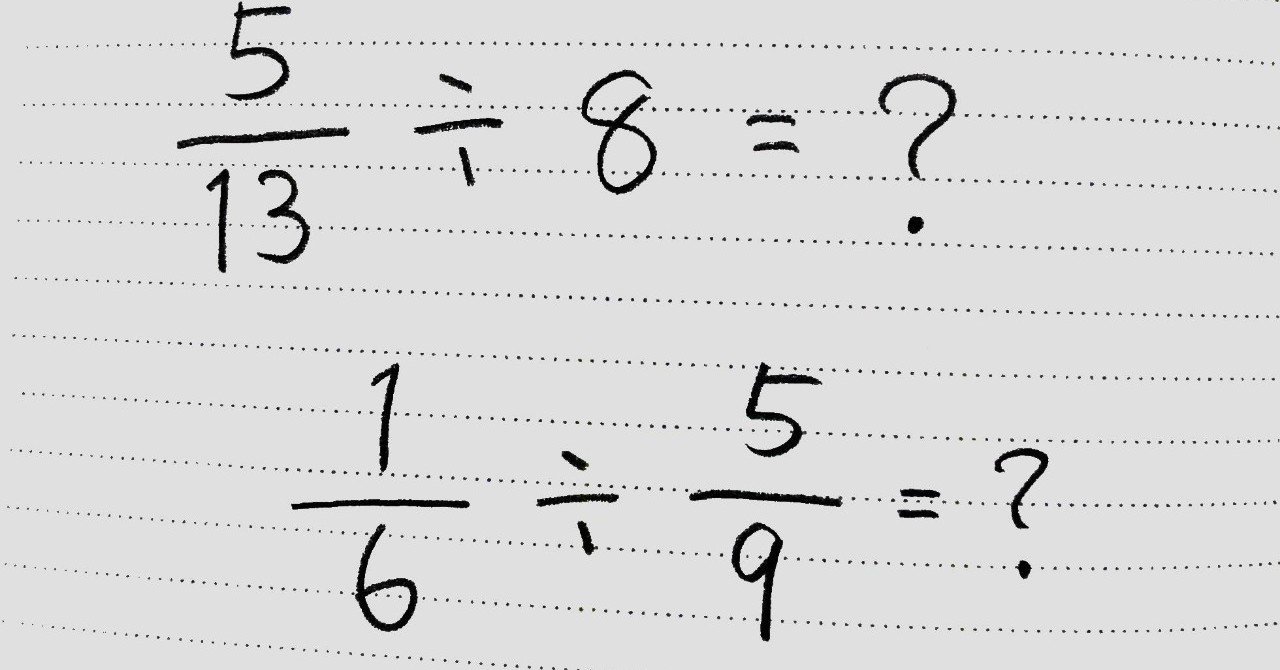



分数を使いこなそう かけ算 わり算と分数 後編 桜花 現役バイト塾講師 Note



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料



1



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料
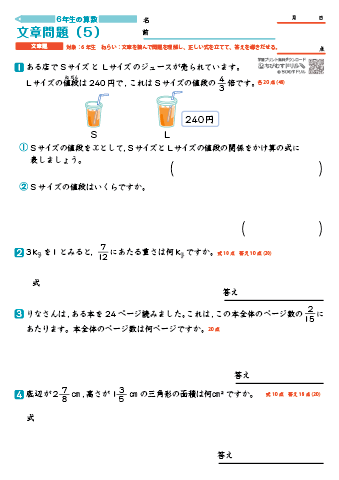



小学6年生 文章問題 文字式 分数の計算 練習プリント テスト ちびむすドリル 小学生




小学6年生の算数 分数のわり算 分数 整数と分数 分数 練習問題プリント ちびむすドリル 小学生




計算まとめ 小数 分数 Youtube
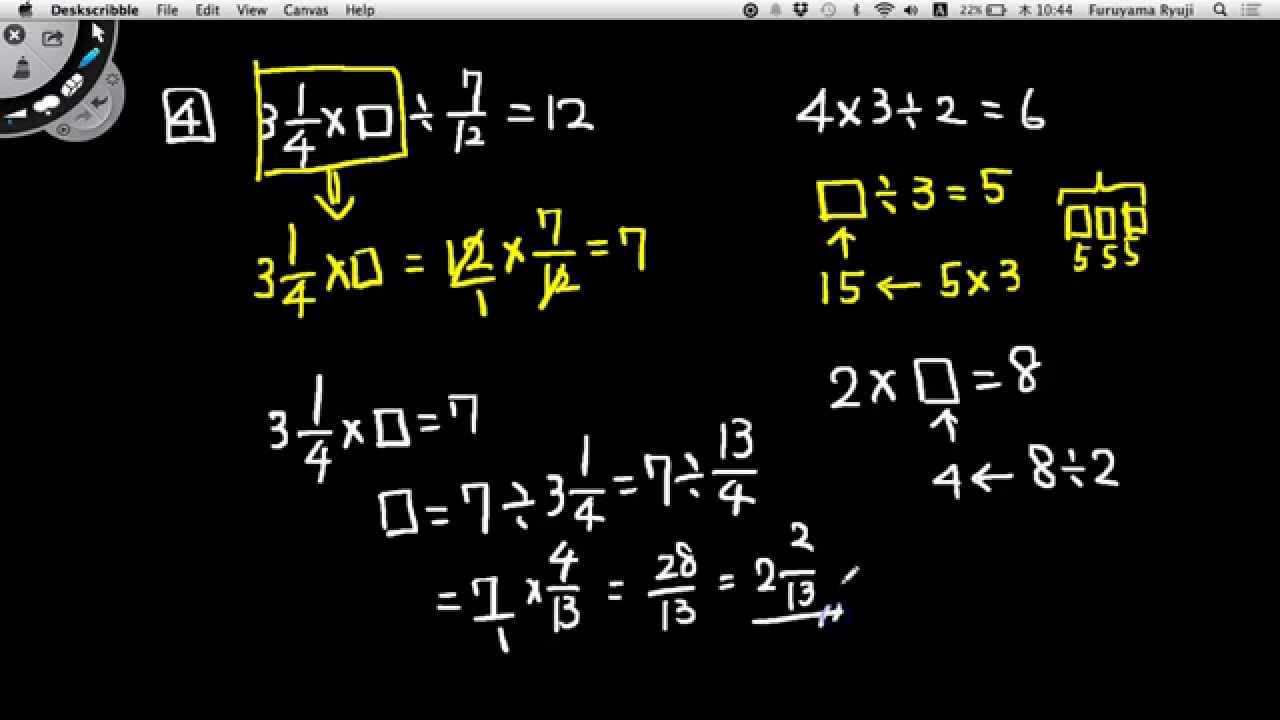



中学受験講座 分数の逆算 Youtube
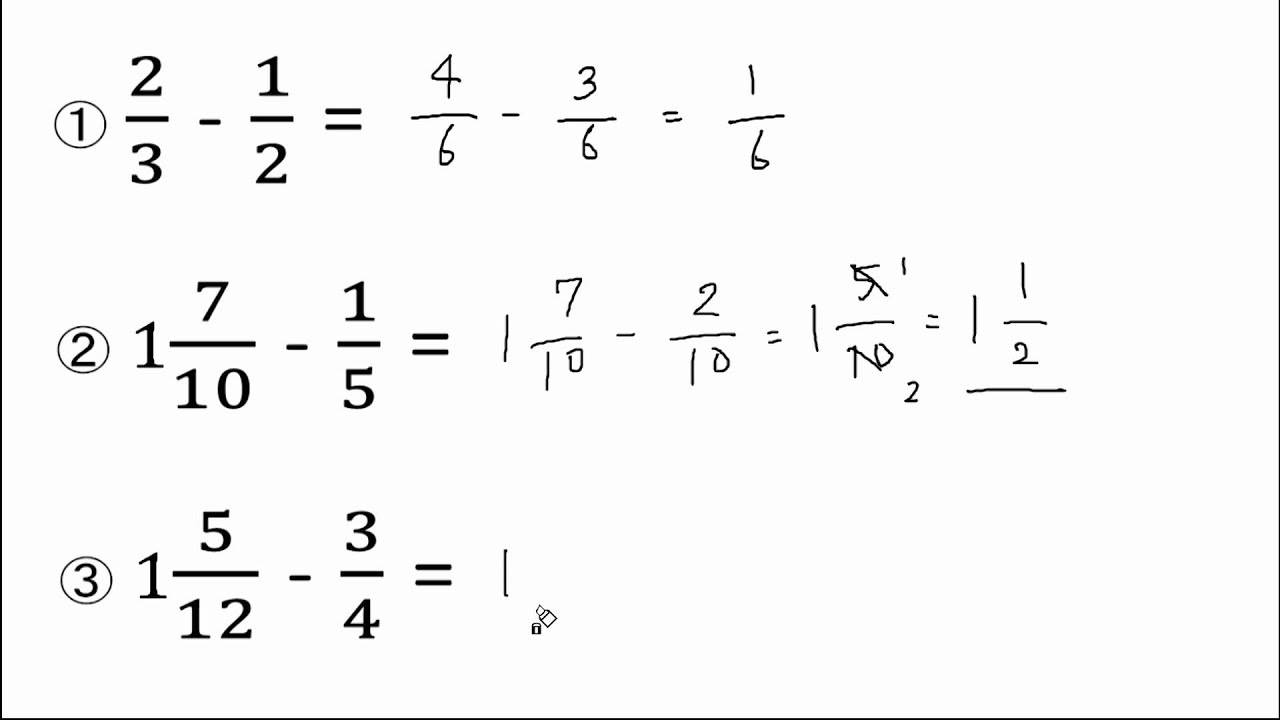



無料印刷可能分数 足し算 引き算 問題 子供のための最高のぬりえ
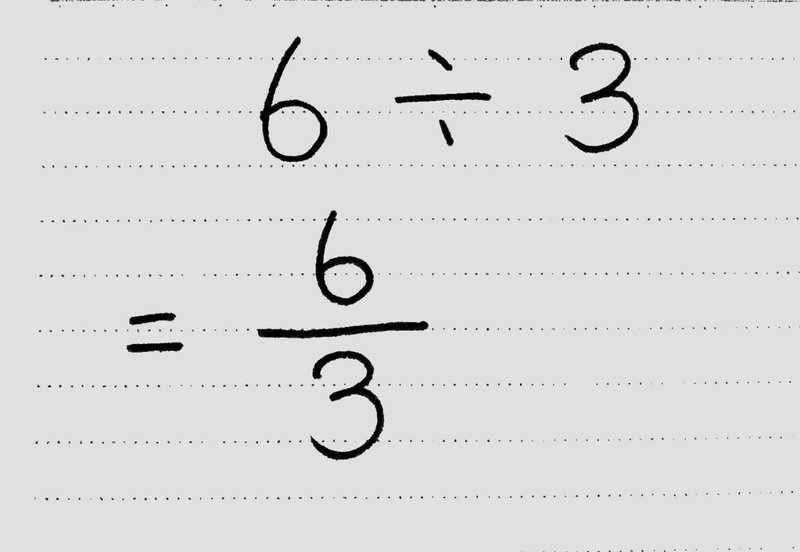



分数を使いこなそう かけ算 わり算と分数 後編 桜花 現役バイト塾講師 Note
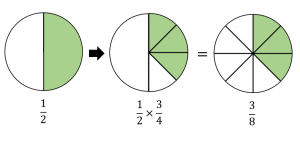



分数のかけ算のやり方と例題5問 具体例で学ぶ数学
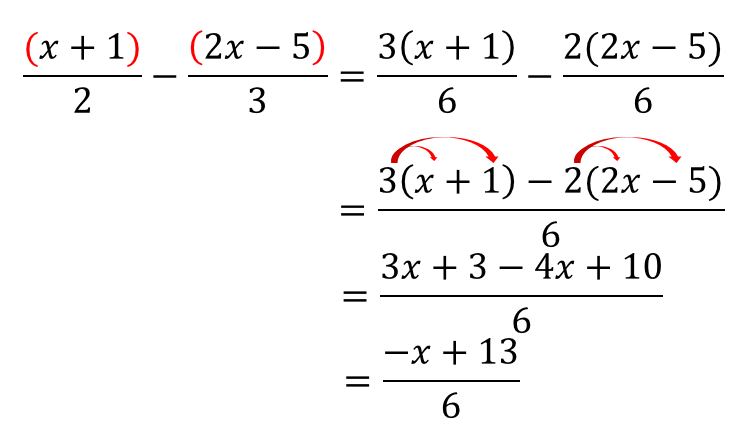



文字式 分数の計算問題を1から丁寧に 数スタ




小学6年生の算数 分数のわり算 分数 整数と分数 分数 練習問題プリント ちびむすドリル 小学生




整数 分数 小数の混じった計算 Youtube



小数と分数が混じった式の解き方 大人の学び直し算数 計算のやり方解説 無料
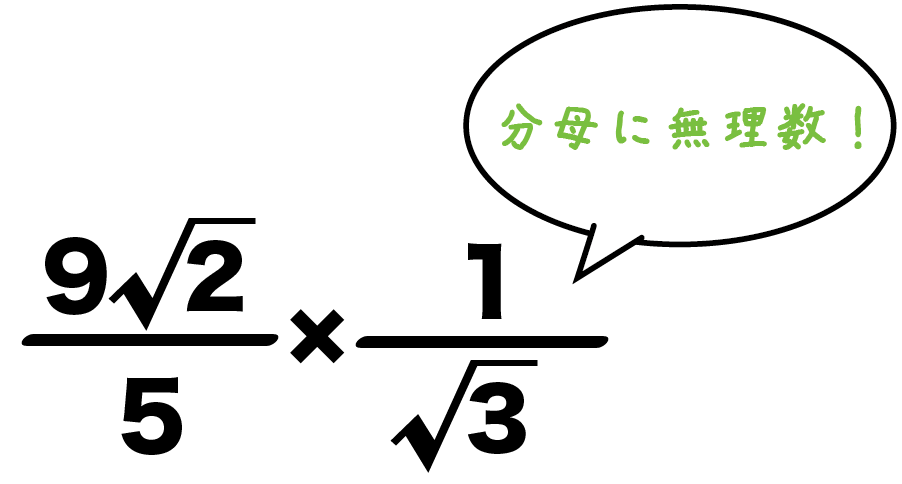



ルート分数の掛け算の計算方法がわかる3ステップ Qikeru 学びを楽しくわかりやすく
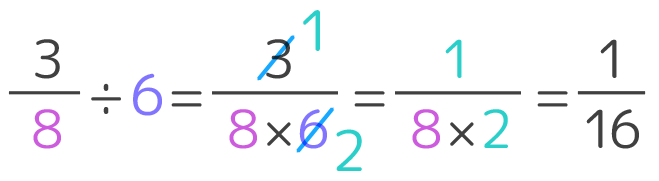



小6 分数と分数の割り算 のやり方は 逆数のかけ算になる理由 そうちゃ式 分かりやすい図解算数 別館



1




中1 P 26 正負の数の計算特訓 Youtube



分数の割り算計算方法の 本質的な意味について なぜ 被除数の分子と Yahoo 知恵袋




分数のかけ算の計算プリント 帯分数編 全240問無料 算数パラダイス




分数 の 分数 の 計算 ニスヌーピー 壁紙
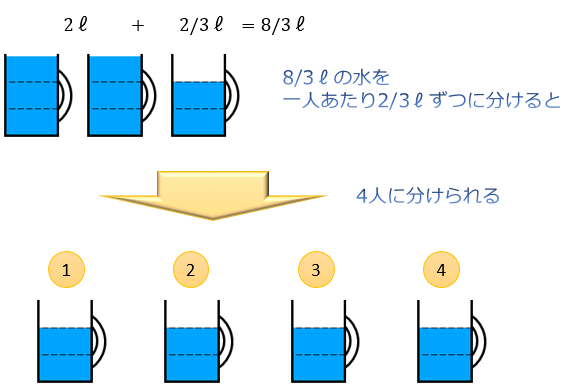



分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ




小6 分数と分数の割り算 のやり方は 逆数のかけ算になる理由 そうちゃ式 分かりやすい図解算数 別館




帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun
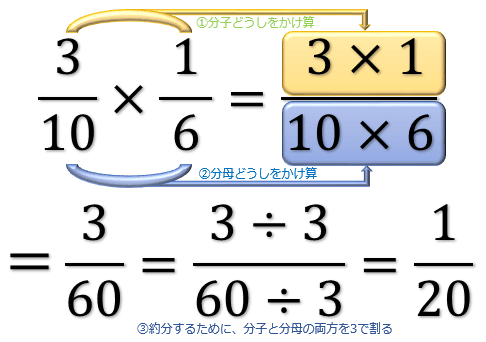



分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ
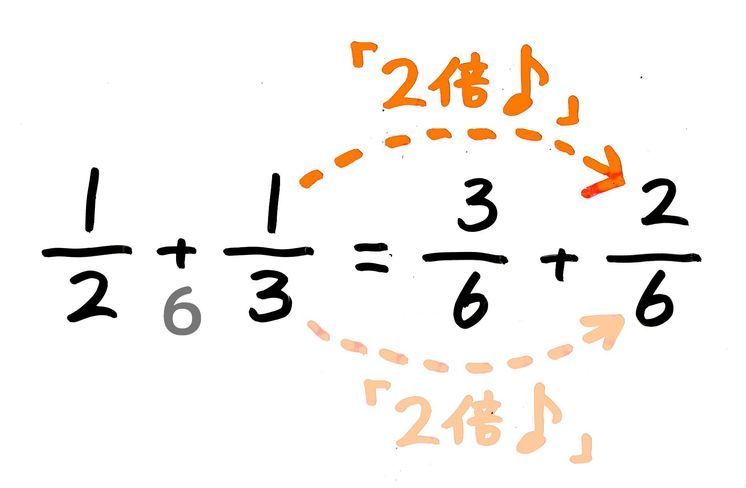



小5 異分母分数の足し算引き算の計算問題のやり方を図解 小6 中学受験生の復習にも そうちゃ式 分かりやすい図解算数 別館



分配法則とは 証明や分数 割り算を含む計算問題 小学生の復習 受験辞典
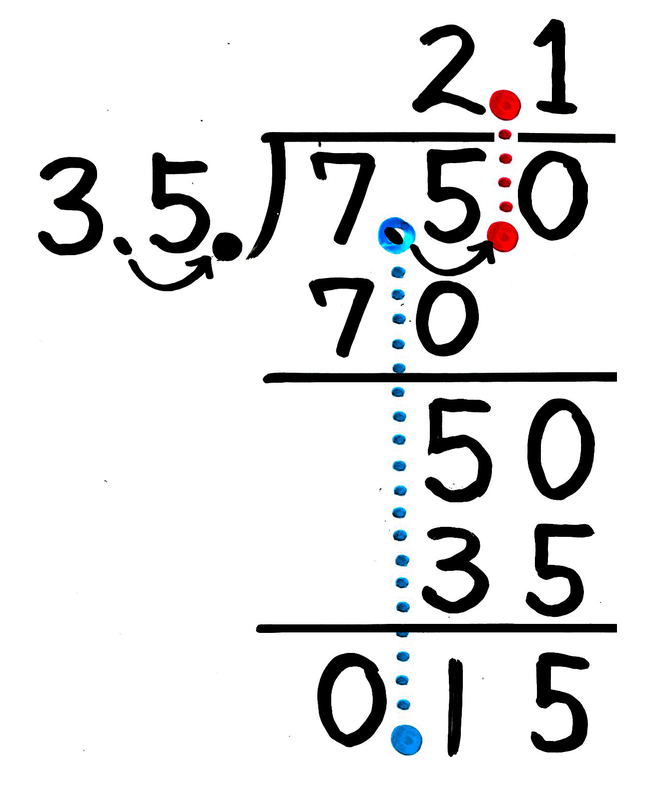



小6 分数と分数の割り算 のやり方は 逆数のかけ算になる理由 そうちゃ式 分かりやすい図解算数 別館




平方根 ルート の割り算の計算方法の5つのステップ Qikeru 学びを楽しくわかりやすく



分数の割り算のやり方 大人の学び直し算数 計算のやり方解説 無料




小学6年生 文章問題 文字式 分数の計算 練習プリント テスト ちびむすドリル 小学生




文字式の割り算の問題 表し方は分数で書くことが多い 中学や高校の数学の計算問題
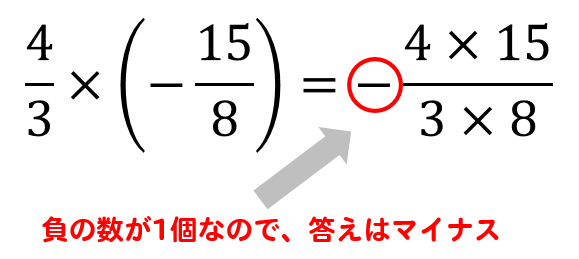



中1数学 正負の数 分数計算のやり方を問題解説 数スタ




分数 足し算 引き算 掛け算 割り算のまざった計算問題 小学生 中学生の勉強




帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun



小数と分数が混じった式の解き方 大人の学び直し算数 計算のやり方解説 無料



分数の掛け算割り算について の3つの計算の仕方の約分の仕方が全くわかり Yahoo 知恵袋
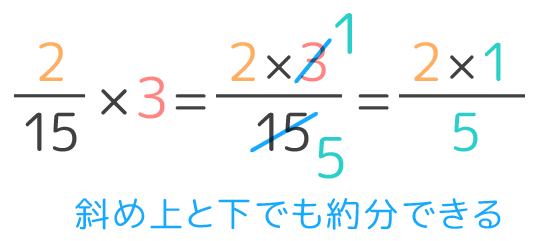



小学5年生 帯 真 分数と整数の割り算 を図解 そうちゃ式 分かりやすい図解算数 別館
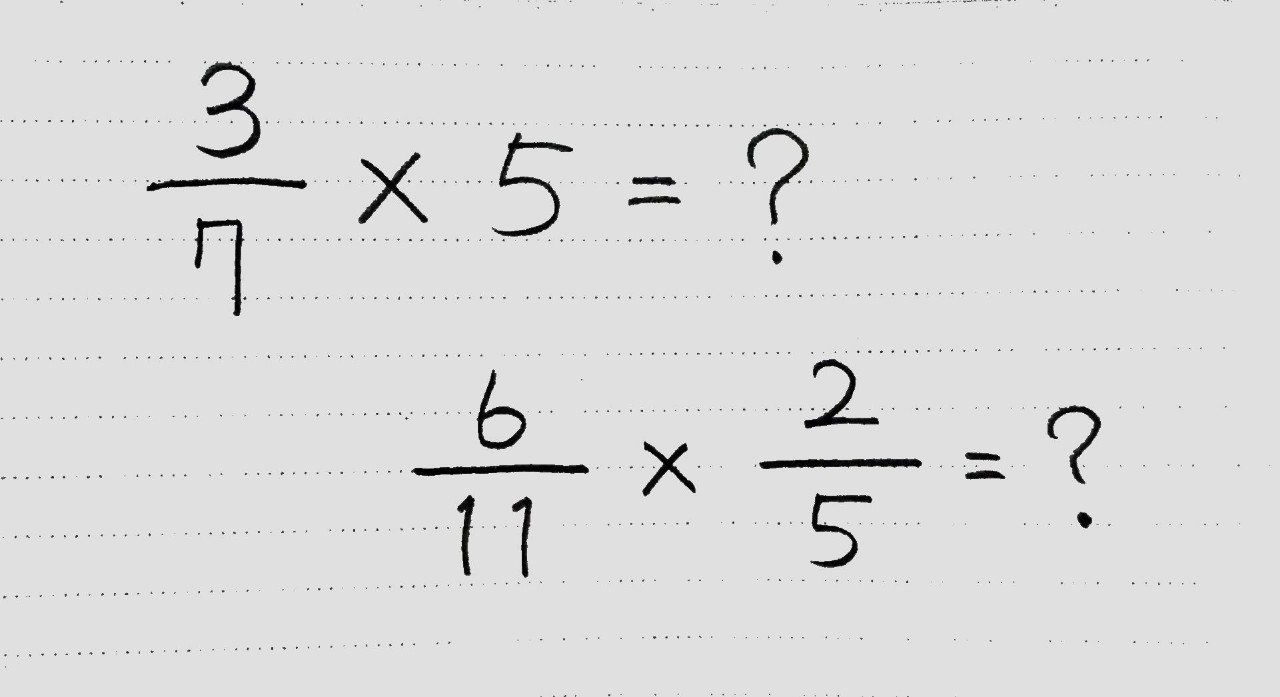



分数を使いこなそう かけ算 わり算と分数 前編 桜花 現役バイト塾講師 Note




分数 掛け算 割り算 問題 ニスヌーピー 壁紙




分数の掛け算 やり方と問題 小学生 中学生の勉強




中1 数学 中1 6 正負のかけ算 わり算 Youtube



すいません 算数の分数の倍と掛け算 割り算で わからないです教 Yahoo 知恵袋




分数の計算 かけ算 割り算 引き算の混合 問題集で 解答は エ 数学 教えて Goo




単項式の乗除 分数の割り算の問題は 分子と分母の分け方に注目 中学や高校の数学の計算問題
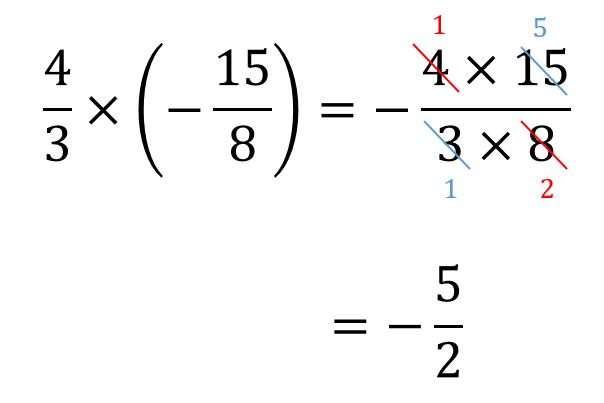



印刷可能 分数 掛け算 割り算 混合 ニスヌーピー 壁紙




分数 掛け算 割り算 問題 ニスヌーピー 壁紙
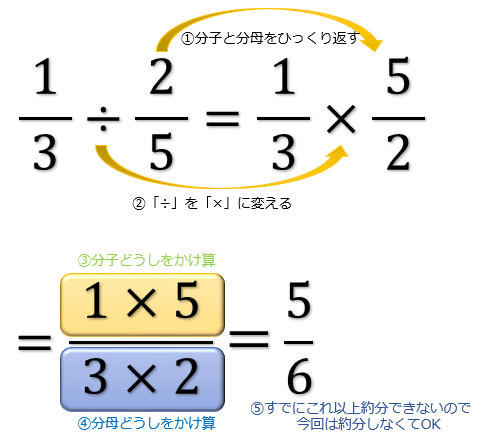



分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ




中1数学 正負の数 分数計算のやり方を問題解説 数スタ




小6への分数の教え方のコツ 計算方法の違いを理解させる かけ算割り算と 算 算 そうちゃ式 分かりやすい図解算数 別館
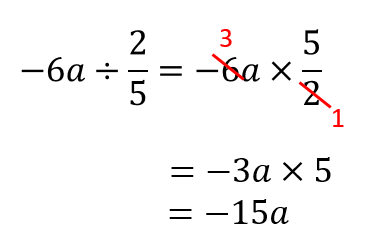



文字式 分数の計算問題を1から丁寧に 数スタ
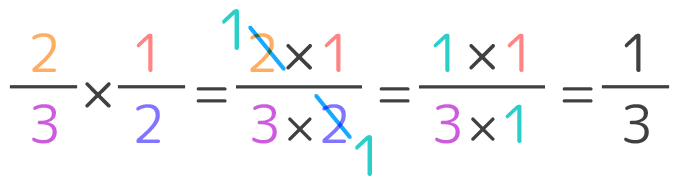



小6 分数と分数の割り算 のやり方は 逆数のかけ算になる理由 そうちゃ式 分かりやすい図解算数 別館



0 件のコメント:
コメントを投稿