A B C ABC ABC の面積を表します。 三平方の定理の三次元空間バージョンです! なお,四平方の定理というと整数論におけるラグランジュの四平方和定理( →整数論の美しい定理7つ の5つ目)のことを指す場合もあるので注意して下さい。 目次 四平方の特集 生徒が喜ぶ「三平方の定理」の授業 提言・「三平方の定理」は面白い教材 この教材を有効に生かすために ・・・・・・ 上垣 渉;A 2 b 2 =c 2 が成り立ちます.(これを 三平方の定理 といいます.) これを用いて3辺の長さのうち2辺の長さが分かっているとき,残りの1辺の長さを求めることができます. 証明 ・・・ 証明の仕方は何十通り~何百通りあると言われています。 中でも簡単そうなのは次の証明です。 《問題1》 次の直角三角形において,xの長さを求めなさい (1)
中3数学 三平方の定理の応用 折り曲げ 2 Youtube
三 平方 の 定理 応用
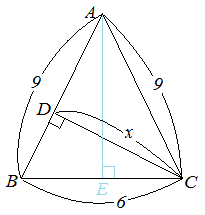
三 平方 の 定理 応用-三平方の定理より 172=h2 h2=264 h2=225三平方の定理を応用すると、正三角形の高さを求めることができる。 例題 右の図のような正三角形の高さ h を求めよ。 (解法) 正三角形 abc の頂点aから底辺bcに垂線ahをおろすと、図のように、点hはbcの中点になる。 なので、まずbhの長さは 1cm である。




國三 Junior High数学的 中学数学 三平方の定理 基礎編 筆記 Clear
三平方の定理a2+b2=c2の証明を、4つの直角三角形を用いて証明させる。4つの合同な直 4つの合同な直 角三角形を使って1つの正方形を作らせ、正方形の面積c 2 と直角三角形の2辺a,bとの関係を幾 三平方の定理の応用問題 ここまでで、三平方の定理の基礎はだいぶ仕上がってきたと思います。 最後に、少しだけ難易度が上がった応用問題を \(2\) 問解いてみましょう。 応用問題①「1 辺と 1 角から辺の長さを求める」7章 三平方の定理 1.プリント ダウンロード レベル 1
平面図形への応用 平面図形への応用 1辺 の長さが 1cm の正方形の対角線の長さを求めてみよう。 対角線の長さを xcm として、三平方の定理を使って求め るよ。 対角線の長さを xcm とすると、 三平方の定理から x 2 = 1 2 +1 2 右下の三角形を見てもらえばわかる通り、正六角形の各頂点から中心に線を引くと三角形ができて、それはすべての角が60°になるから、正三角形だね! 正三角形ということは、すべての辺の長さが等しい。 つまり、下図のようになるよ! ということは、各頂点から点Pまでの長さが 6 6 だから、三平方の定理を用いると、 x2 = 62 –22 x 2 = 6 2 – 2 2 ∴ x2 = 36− 4 = 32 x 2 三平方の定理(ピタゴラスの定理)の応用問題パターン10選 三平方の定理(ピタゴラスの定理)は、直角三角形において成り立つ定理です。 また、どんな定理だったかと言うと、$3$ 辺の長さについての定理でした。
数学史から入る「三平方の定理」 「三平方の定理」は,いつ,どのようにして発見されたか ・・・・・・ 片野 善一郎三平方の定理 発展問題まとめ お疲れ様でした! 入試などの発展問題では、今回のように 三平方の定理を使って、方程式を作ることで 長さを求めていくようになります。 まずは、求めたい部分を とする。 直角三角形の各辺を を使って表すことがピタゴラス数 a 2 b 2 = c 2 を満たす自然数の組 (a, b, c) をピタゴラス数またはピタゴラスの三つ組数 (Pythagorean triple) という。 特に、 a, b, c が互いに素であるピタゴラス数 (a, b, c) を原始的 (primitive) あるいは素 (coprime) であるといい、そのようなピタゴラス数は原始ピタゴラス数 (primitive Pythagorean



3




無料 中3数学 発展 応用問題 解答プリント 336 三平方の定理4 空間図形
が成り立ちます。これで、三平方の定理を証明することができました!「平方」とは 2乗のことなので、「三平方の定理」と言われるゆえんは、直角三角形の「三」つの辺それぞれの「平方」、つまり a 2, b 2, c 2 の間に成り立つ関係式ということですね。の定理」を利用して 求められることに関 、定理を活 用しようとしている。 ・直角三角形の三辺の長 さの間に成り立つ関係 や、「三平方の定理」 を用いて直角三角形の うちの一辺の長さを求 め、平面図形や空間図 形の性質を考えるな ど、数学的な見方や考弦定理を始め、種々の証明を 村守 隆男 著 「トレミーの定理について」 を参考にさせて頂きました。村守先生は、私の研究室の斜め向かいの研究室におられた方 で、懐かしいです...! プトレマイオスの定理の応用例
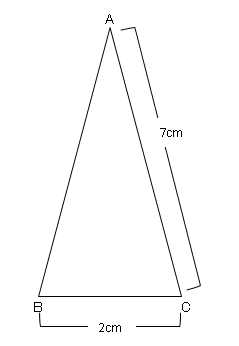



三平方の定理の応用 2 ネット塾




三角柱の体積を求める問題です 三平方 ピタゴラスの定理の応用です 解ける方解き方 Clear
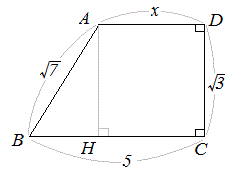
三 平方 の 定理 三平方の定理 中 3 数学 三 平方 の 定理 現在小6生のみ小5・3月号以前に<チャレンジタッチ>を受講されたことのある場合、1月号教材とあわせて、進研ゼミ専用タブレット「チャレンジパッド2」をお届けします。平面図形,空間図形の問題で三平方の定理を使って解くときに,補助線をどうひけばよいのかわかりません。 進研ゼミからの回答 図形の中に「直角三角形」ができるように補助線をひきます。 直角をつくることができる 三 平方 の 定理 応用 問題 解答 下の図のように補助線をひき、左の直角三角形に 三平方の定理を用います。 \\(x^2=2^28^2\\) \\(x^2=68\\) \\(x=±\\sqrt{68}\\) \\(=±2\\sqrt{17}\\) この問題では、当然 \\(x\\) は正の値なので \\(x=2\\sqrt{17}\\) 例題2 下の図の、\\(x\\) の値を求めなさい。




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




國三 Junior High数学的 中学数学 三平方の定理 基礎編 筆記 Clear
三 平方 の 定理 応用 三 平方 の 定理 応用 解き方 三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。 数学史から入る「三平方の定理」 「三平方の定理」は,いつ,どのようにして発見されたか ・・・・・・ 片野 善一郎正解率 \ (0三平方の定理の三次元拡張 今星の大学入試でも京都府立大で 出題されている。過去にも名古屋大、 広島大、朁京大などで類題が出された。 いずれも誘導文つきで、予備知識なしで 取り組めるよう配慮されている。 s2= 2 s1 2 s2 2 s3三平方の定理(基本問題1) 例題 次の直角三角形で、xの値を求める。 x 2 6 xが斜辺なので 2 2 6 2 = x 2 x 2 = 40 x = ±2 √ 10 x > 0より x =2 √ 10 x 4 5 斜辺が5なので x 2 4 2 =5 2 x 2 = 2516 x 2 =9 x=±3 x>0より x=3 次の直角三角形で、xの値をそれぞれ求めよ。
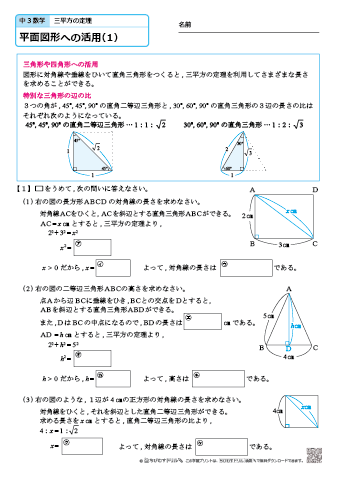



中学3年生 数学 三平方の定理 平面図形への活用 練習問題プリント ちびむすドリル 中学生




中3の数学の問題 セルモ大蔵 世田谷 の塾長ブログ
三平方の定理が使えるのは直角三角形である。 定理を利用する場合は図から直角三角形を探すか、補助線を書いて直角三角形を作る。 座標上での2点間の距離 いままで、座標上で斜めの長さは出せなかったが、三平方の定理を使えば出せるようになる。 a bを得るというものである.公式の中の「-2bccos・A」の意味が直観的に把握され,また三 平方の定理が余弦定理の特別な場合であることが実感されるであろう. 4.3 相似比を用いた証明122 整数は四つの平方数の和に分解することができる 定理15 全ての正の整数は、四つの平方数の和として表わすことができる n = x2 1 x 2 2 x3 x 2 4 上の定理において02 = 0 も平方数と考えている。よって、0 を除くならば四つ以 下の平方数の和というべき




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース
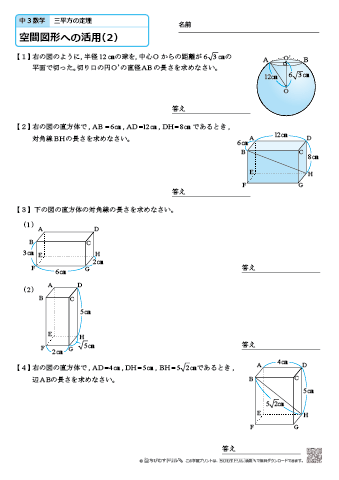



中学3年生 数学 三平方の定理 空間図形への活用 練習問題プリント ちびむすドリル 中学生
三平方応用 折り返し 折り目FGの長さを求める。 A B C D E F G 12cm 18cm 直角三角形ABGで三平方の定理を用いてAGとBGを求める。 AG=xcmとする。 AGはCGを折り返した線分なのでBG= (18x)cmとなる。 A B C D E F G 12cm 18cm P 13cm 5cm 8cm 12cm FからBCに垂線FPを引く。った具体的な場面で,三 平方の定理を利用しよう としている。 E (応用) 学びに向かう力 三平方の定理を,生活に いかすために,新たな活動 を創り出そうとしている。 未知の状況への対応 学びを生かそうとする力 いままで求めることのでき 三平方の定理を使い2点間の距離を求める問題です。 三平方の定理が使えると図形の問題を解ける幅が広がります。 どんどん使っていきましょう。 記事を読む




中3数学 三平方の定理とは 例題編 映像授業のtry It トライイット




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 2 4
4 三平方の定理の応用問題 5 底面の半径が 2 cm,母線の長さが 8 cm の円錐について,次の問いに 答えよ。 ⑴ 側面の展開図のおうぎ形の中心角を求めよ。 ⑵ 右の図のように,円錐の側面上をまわるように,点 A から点 A ま でひもをかける。从 1730 年至 1770 年, 在大约四十年的时间里 Euler 证明了许多与四平方定理有关的结果, 为后来这一定理的证明创造了条件, 但他本人却很遗憾地未能率先证明这一定理 注三 。 1770 年, 法国数学家 Joseph Lagrange () 以 Euler 的一个结果为基础, 率先给出了三平方の定理 直角三角形の3辺の 長さの間に成り立つ 関係に着目し,三平 方の定理を見いだす ことができる。 三平方の定理 の利用 図形の中に直角三 角形を見いだし, 三平方の定理を用 いることで図形の 性質などを考える ことができる。
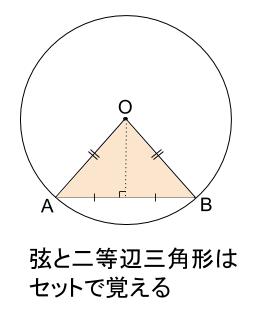



中学数学 三平方の定理 円と接線 弦 中学数学の無料オンライン学習サイトchu Su




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
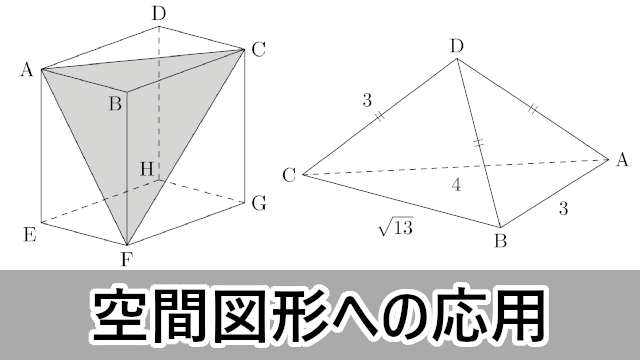



数学ia 空間図形の応用問題 広島工業大 東京慈恵会医科大 大学入試数学の考え方と解法
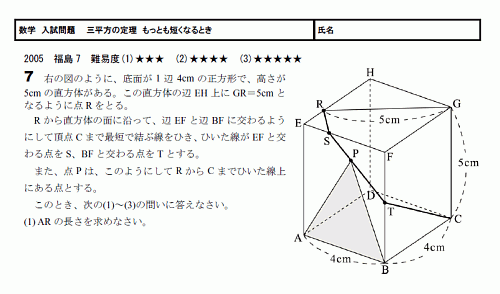



三平方の定理 スタディーx




知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より




三平方の定理 応用問題 関数




数学 中3 61 三平方の定理 基本編 Youtube



1




中3数学 三平方の定理の応用 折り曲げ 2 Youtube
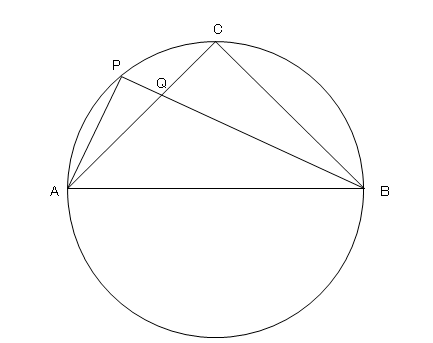



三平方の定理の応用 3 ネット塾



Studydoctor三平方の定理の利用 中学3年数学 Studydoctor




中3数学 三平方の定理の応用 三角形の面積 見方を変える Youtube




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理の応用問題 中学3年数学 Youtube
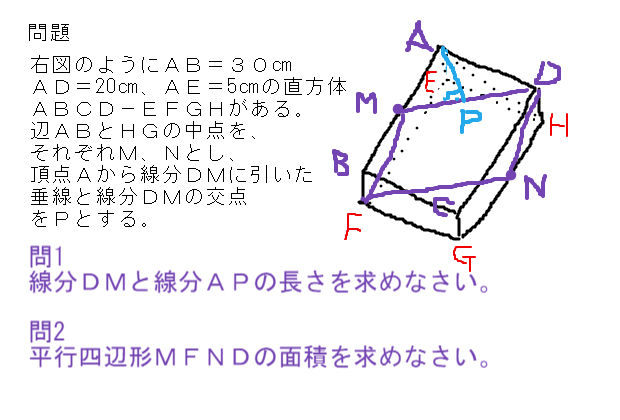



図形での三平方の定理の応用問題 正答率22 中学数学 理科 寺子屋塾の復習サイト




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理 ピタゴラスの定理 の例題や計算のやり方 証明 応用 難問などのまとめはこちらです 行間 ぎょうのあいだ 先生




無料 中3数学 発展 応用問題 問題プリント 334 三平方の定理2



中3数学 三平方の定理3 三平方の定理 すべて無料 星組の中学数学講座
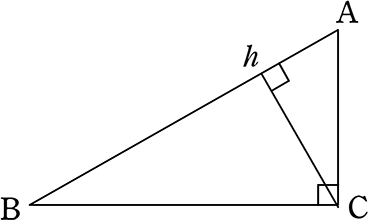



中学数学 三平方の定理
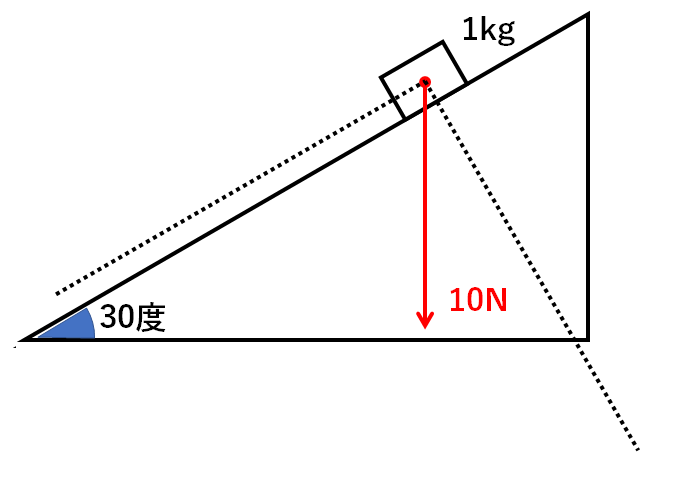



中3物理 分力と三平方の定理 中学理科 ポイントまとめと整理



三平方の定理の応用



1




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



三平方の定理の応用
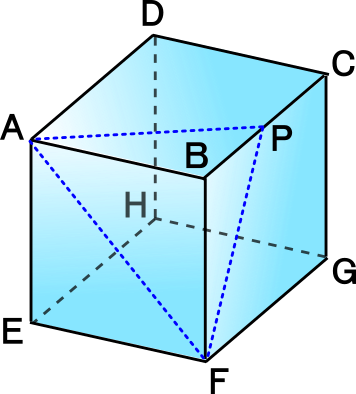



中学3年数学練習問題 三平方の定理 空間図形への応用 2
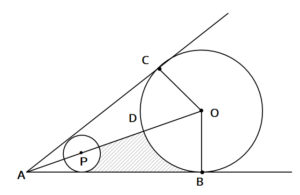



中3数学応用 おうぎ形と三平方の定理の練習問題 中学生勉強サイトあかね先生



Studydoctor三平方の定理と四角形への利用 中学3年数学 Studydoctor




特別な直角三角形 前半 三平方の定理応用 中学生と学ぶ 4 無料教材付き 中3 数学 Youtube




無料 中3数学 発展 応用問題 問題プリント 333 三平方の定理1




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース
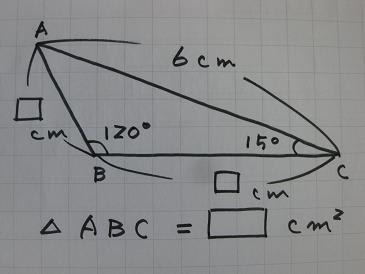



マッキーの教室 中2生徒の 三平方の定理 問題の質問に答える マッキーのつれづれ日記




中3数学 三平方の定理とは 練習編 映像授業のtry It トライイット




数学 三平方の定理の応用 Youtube




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生
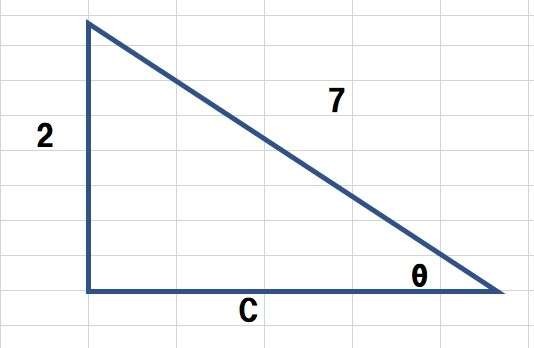



数学 三平方の定理を5秒で計算する裏ワザ 見ないと損する 予備校なら武田塾 京成佐倉校



Studydoctor三平方の定理の応用問題 中学3年数学 Studydoctor




三平方の定理と相似の問題 無料で使える中学学習プリント
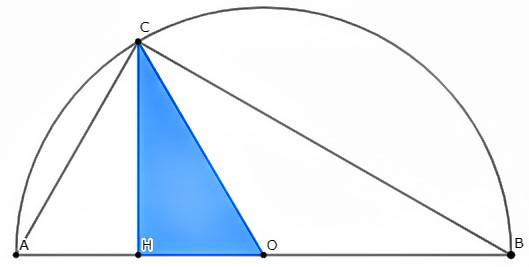



ファイル 三平方の定理 Jpg Wikipedia




中3数学 三平方の定理の応用 75度に要注意 Youtube




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




Mathematics 三平方の定理 3 いろいろな三角形 働きアリ
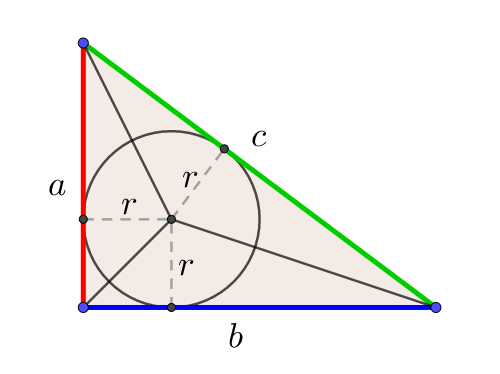



三平方の定理の証明4 直角三角形と内接円 キソカラ



Mathematics 高校入試問題研究 数学 3 大阪府公立高校入試 前期 理数科 平成21年度 働きアリ The 2nd
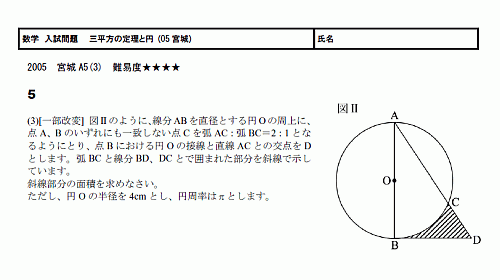



三平方の定理と円 スタディーx




三平方の定理を利用して四角すい 円すいの体積を求める 無料で使える中学学習プリント




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導
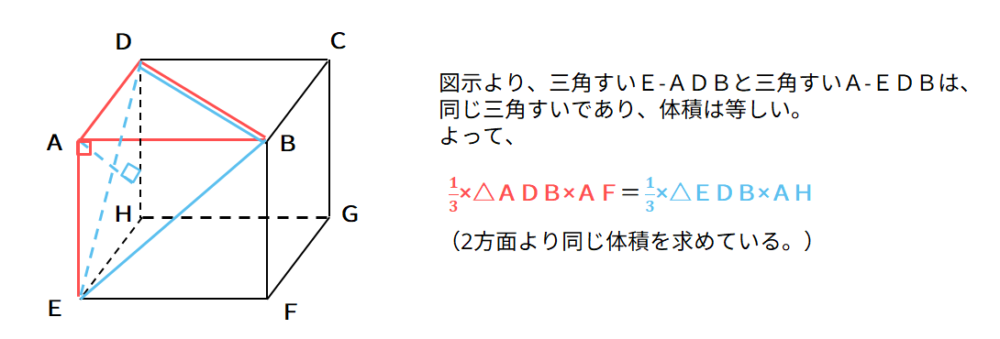



高校入試対策数学 空間図形と三平方の定理の対策問題 中学生勉強サイトあかね先生




中学受験算数 等積変形の利用 ヒポクラテスの月
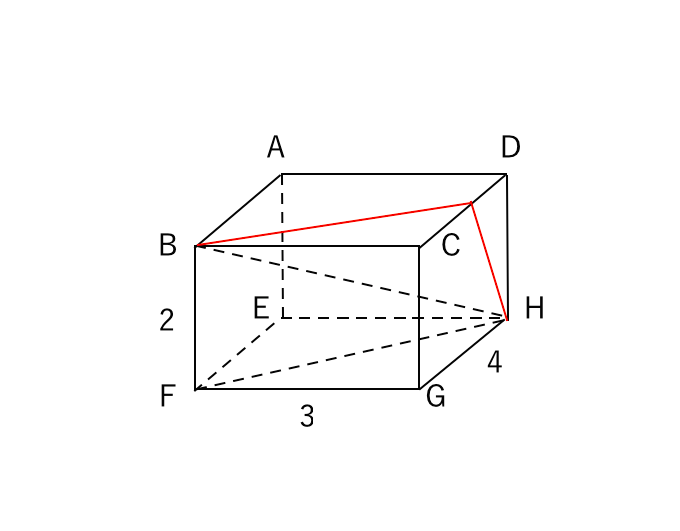



三平方の定理 立体 苦手な数学を簡単に



Studydoctor特別な三角形と三平方の定理 中学3年数学 Studydoctor
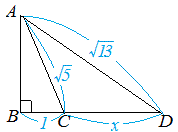



三平方の定理の応用




無料 中3数学 発展 応用問題 解答プリント 334 三平方の定理2




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




数学で習った ピタゴラスの定理 三平方の定理 や 三角測量 が身近に溢れていた件 Itをもっと身近に ソフトバンクニュース
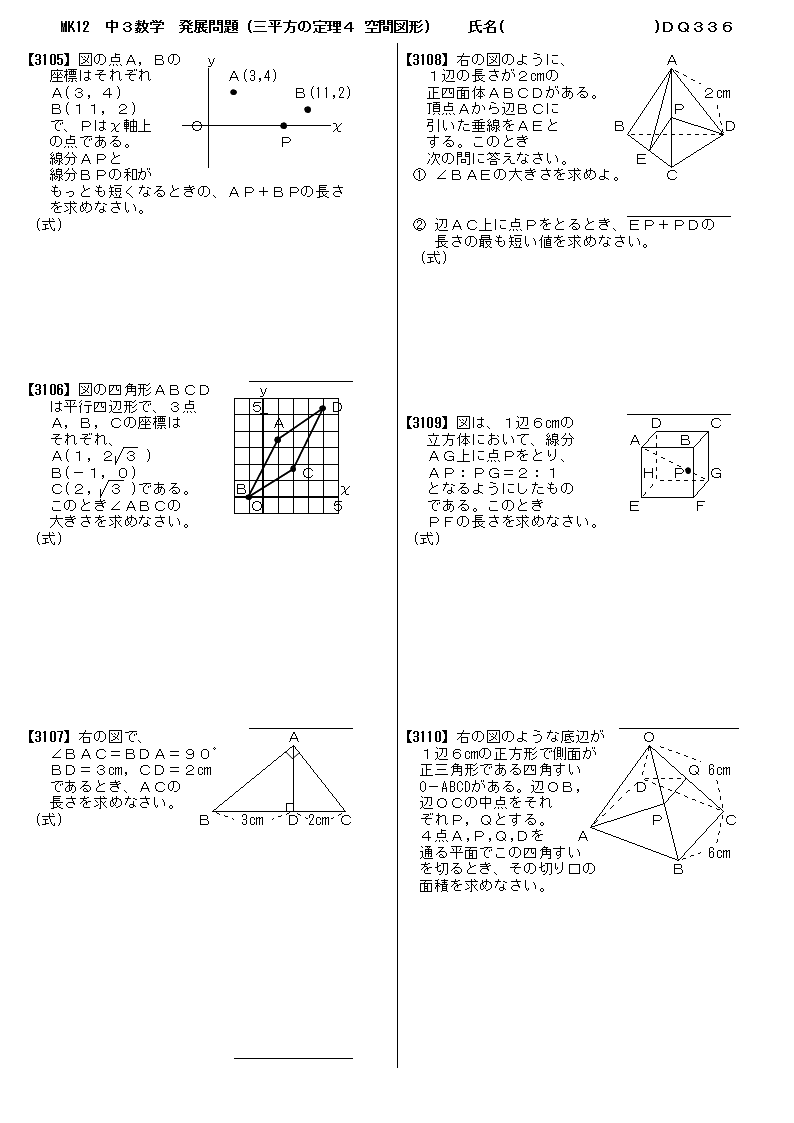



無料 中3数学 発展 応用問題 問題プリント 326 三平方の定理4 空間図形
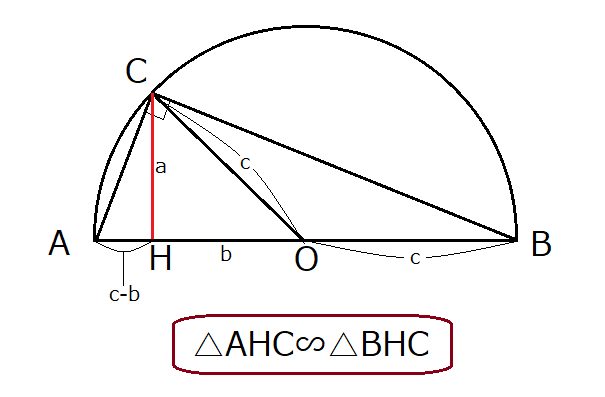



三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋
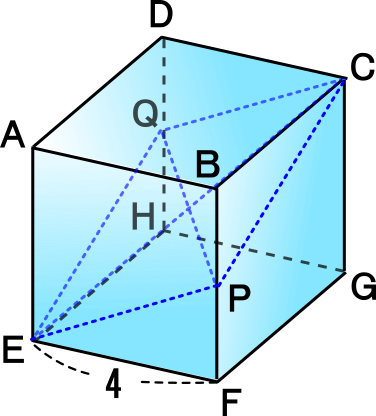



中学3年数学練習問題 三平方の定理 空間図形への利用 2



三平方の定理の応用問題です 解説に解き方が載っていなか Yahoo 知恵袋



三平方の定理
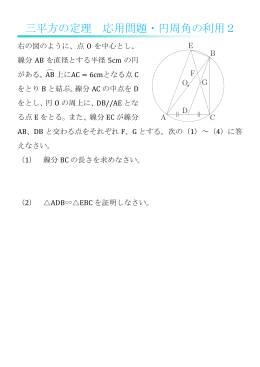



三平方の定理 応用問題 関数
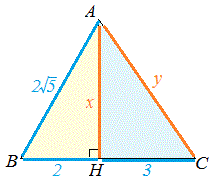



三平方の定理の応用




三平方の定理 平面図形のいろいろな応用問題 無料で使える中学学習プリント




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張
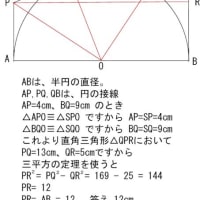



知っていて当たり前 三平方の定理の応用 名寄 算数数学教室より




中学数学 三平方の定理を利用する難問 応用 丁寧な解説 なぜか分かる はかせちゃんの怪しい研究室




三平方の定理で辺を求める Youtube




三平方の定理の応用問題 中学3年数学 Youtube




三平方の定理の応用 イ弋マ本ゼミナール




世界が変わる裏技 三平方の定理を5秒で計算するテクニック Youtube




三平方の定理 応用問題 関数



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




三平方の定理と方程式 Youtube




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4
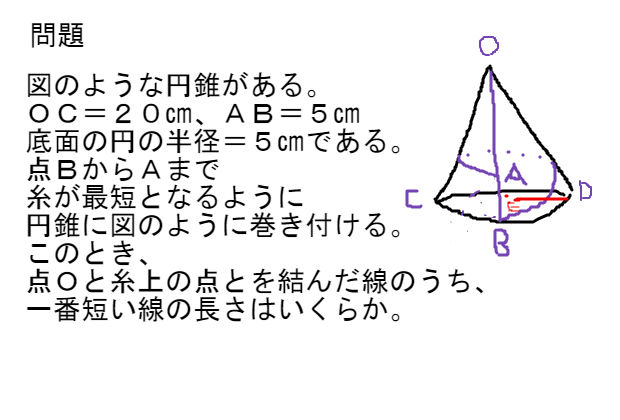



円錐と三平方定理の応用問題 総合力ためし 制限4分 中学数学 理科 寺子屋塾の復習サイト



Studydoctor三平方の定理と色々な三角形の面積 中学3年数学 Studydoctor



1




三平方の定理の応用



Homeroom 数学の入試問題を解くとき大切なこと 正しい入り口から入らないと問題は解けない 空間図形 三平方の定理 働きアリ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
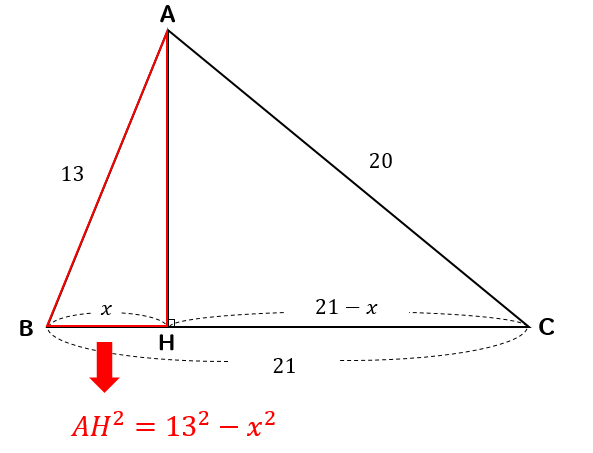



三平方の定理 方程式を利用する発展問題を解説 数スタ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
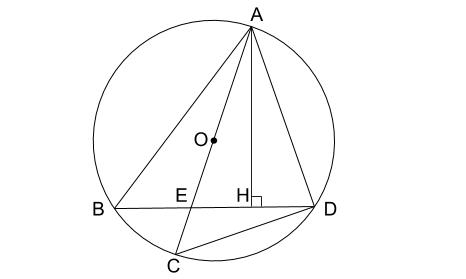



高校入試数学の難問 円 相似と三平方の定理の総合 中学数学の無料オンライン学習サイトchu Su




中3数学 三平方の定理の応用 三角形の面積 見方を変える Youtube




円を利用した三平方の定理の証明 数学の面白いこと 役に立つことをまとめたサイト



三平方の定理の応用 まとめ1 中学から数学だいすき




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
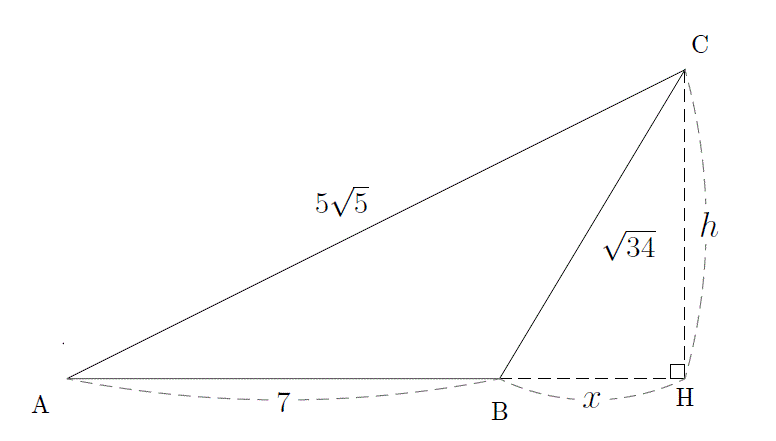



かみのドリル 三平方の定理



0 件のコメント:
コメントを投稿